Luca Pacioli’s Summa de arithmetica (Venice, 1494).the Arte dell’Abbaco, an anonymous text published in the Venetian dialect in 1478, often called the Treviso Arithmetic because it was printed in Treviso, just inland from Venice, Italy.
Jamshīd al-Kāshī’s Miftāḥ al-ḥisāb (Samarqand, 1427), in which the numerals used are sexagesimal (base 60), and the grid is turned 45 degrees to a “diamond” orientation. Other notable historical uses of lattice multiplication include: Swetz compares and contrasts multiplication by gelosia (lattice), by scacherii (chessboard), and other tableau methods. This is in contrast to lattice multiplication, a distinctive feature of which is that each cell of the rectangle has its own correct place for the carry digit this also implies that the cells can be filled in any order desired. In this technique, the square cells are not subdivided diagonally only the lowest-order digit is written in each cell, while any higher-order digit must be remembered or recorded elsewhere and then "carried" to be added to the next cell. In Chapter 3 of his Liber Abaci, Fibonacci does describe a related technique of multiplication by what he termed quadrilatero in forma scacherii (“rectangle in the form of a chessboard”). In fact, however, no use of lattice multiplication by either of these two authors has been found. 825) or by Fibonacci in his Liber Abaci (Italy, 1202, 1228). It is sometimes erroneously stated that lattice multiplication was described by Muḥammad ibn Mūsā al-Khwārizmī (Baghdad, c. This is reinforced by noting that the Arabic term for the method, shabakh, has the same meaning as the Italian term for the method, gelosia, namely, the metal grille or grating (lattice) for a window. The mathematician and educator David Eugene Smith asserted that lattice multiplication was brought to Italy from the Middle East. in Chinese mathematics was by Wu Jing in his Jiuzhang suanfa bilei daquan, completed in 1450. in European mathematics was by the unknown author of a Latin treatise in England, Tractatus de minutis philosophicis et vulgaribus, c. in Arab mathematics was by Ibn al-Banna' al-Marrakushi in his Talkhīṣ a‘māl al-ḥisāb, in the Maghreb in the late 13th century. The earliest recorded use of lattice multiplication: It is being researched where it arose first, whether it developed independently within more than one region of the world. Though lattice multiplication has been used historically in many cultures, a method called 'Kapat-sandhi' very similar to the lattice method is mentioned in the commentary on 12th century 'Lilavati' a book of Indian mathematics by Bhaskaracharya. įolios 9v and 10r from the manuscript "Raqâiq a-haqâiq fi hisab ad-daraj wa ad-daqâiq", from the Bibliothèque nationale de France, showing lattice multiplications with old Arab numerals If the simple product lacks a digit in the tens place, simply fill in the tens place with a 0. Write their product, 10, in the cell, with the digit 1 above the diagonal and the digit 0 below the diagonal (see picture for Step 1). In this case, the column digit is 5 and the row digit is 2. After writing the multiplicands on the sides, consider each cell, beginning with the top left cell. Then each cell of the lattice is filled in with product of its column and row digit.Īs an example, consider the multiplication of 58 with 213. 
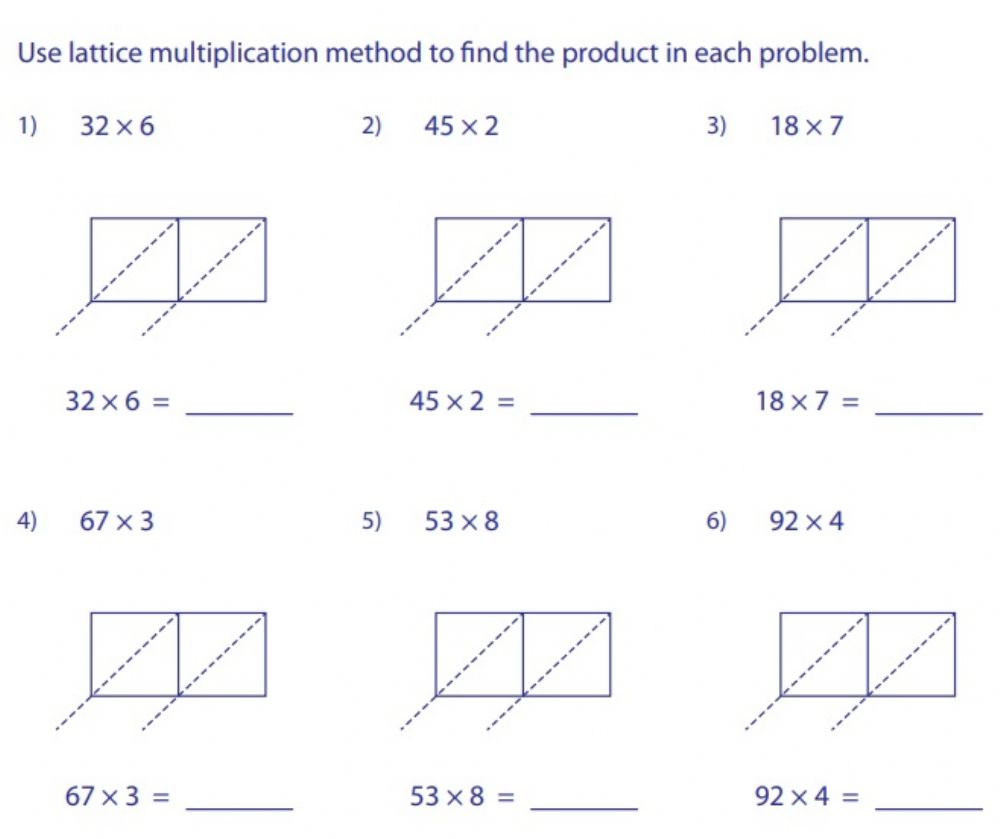
The two multiplicands of the product to be calculated are written along the top and right side of the lattice, respectively, with one digit per column across the top for the first multiplicand (the number written left to right), and one digit per row down the right side for the second multiplicand (the number written top-down). A grid is drawn up, and each cell is split diagonally.
0 kommentar(er)
